|
デザイン >デジタルFIRフィルタ |
フィルタは信号に含まれるノイズを除去する目的で使用されます。
フィルタは大きく分類してアナログフィルタ、デジタルフィルタの二種類に分類されます。
アナログフィルタ:
デジタルフィルタ:
フィルタは大きく分類してアナログフィルタ、デジタルフィルタの二種類に分類されます。
アナログフィルタ:
ハム除去フィルタなどオペアンプを使用した低周波から、コイルを使用した高周波周波数帯までをカバーします。
一度、作製されたフィルタのカットオフ周波数は、通常変更できません。
一度、作製されたフィルタのカットオフ周波数は、通常変更できません。
デジタルフィルタ:
一度エリアシングフィルタを通過したあとの電圧情報などをCPUに数値としてサンプリングします。
CPUの処理能力、サンプリング周波数に影響を受け、使用する周波数帯域に制限があります。
取り込んだ音声データなどに対して、数学的にプログラムである周波数の音のみを除去したり、
ノイズ成分を除去したりします。
画像処理フィルタでは主に空間フィルタを使用して画像ノイズの除去、画像の鮮明化等に使用します。
プログラムですのでフィルタの特性を変更する事ができます。
多種多様のデジタルフィルタがありますが、ここではFIRデジタルフィルタのローパスフィルタの使い方を記載します。
CPUの処理能力、サンプリング周波数に影響を受け、使用する周波数帯域に制限があります。
取り込んだ音声データなどに対して、数学的にプログラムである周波数の音のみを除去したり、
ノイズ成分を除去したりします。
画像処理フィルタでは主に空間フィルタを使用して画像ノイズの除去、画像の鮮明化等に使用します。
プログラムですのでフィルタの特性を変更する事ができます。
多種多様のデジタルフィルタがありますが、ここではFIRデジタルフィルタのローパスフィルタの使い方を記載します。
FIR(Finit Impulse Response)フィルタは、インパルス応答が有限長であるフィルタをいいます。
その特徴は、
その特徴は、
1.インパルス応答の中心に対し、インパルス応答の係数を左右対称にすると完全直線位相特性を実現できる。
群遅延特性が、全周波数帯域でフラットになり、位相歪みが起きない。
2.FIRフィルタは非巡回型であるため、インパルス応答の係数の値に関わらず、常に安定である。
3.急峻な遮断特性を得るには、次数を高くする必要があるため、演算量が増大し処理速度の低下を招く。
群遅延特性が、全周波数帯域でフラットになり、位相歪みが起きない。
2.FIRフィルタは非巡回型であるため、インパルス応答の係数の値に関わらず、常に安定である。
3.急峻な遮断特性を得るには、次数を高くする必要があるため、演算量が増大し処理速度の低下を招く。
FIRフィルタのブロックダイア
下記は、上記ブロックダイヤに単位パルスを入力した時の応答波形です。
FIRフィルタをZ変換して、出力/入力を求めると伝達関数が求まります。
h(z)= h0+h1Z-1+・・・+hnZ-n
ここで、N=4とし、Z = ejωTを代入して周波数特性を求めると、
h(ejωT)= h0+h1e-jωT+h2e-j2ωT+h3e-j3ωT+h4e-j4ωT
インパルス応答の係数の中心に対し、係数が対称となるように係数を与えると、
h(ejωT)= h0+h1e-jωT+h2e-j2ωT+h1e-j3ωT+h0e-j4ωT
= e-j2ωT(h0ej2ωT+h0e-j2ωT)+e-j2ωT(h1ejωT+h1e-jωT)+h2e-j2ωT
= e-j2ωT( 2h0cos(2ωT)+2h1cos(ωT)+h2 )となります。
= e-j2ωT( 2h0cos(2ωT)+2h1cos(ωT)+h2 )となります。
ところで、e-jωT = cos(ωT)-jsin(ωT) なので、
上記e-jωTの振幅特性は全周波数領域にわたり1となり、位相特性はωに比例して直線位相となります。
N=4のFIRフィルタは、-2ωTの直線位相特性となります。
2h0cos(2ωT)+・・・)は複素数でなく実関数なので、振幅を表します。
FIRフィルタの周波数特性は、そのFIRフィルタのインパルス応答のフーリエ変換で与えられ、逆にFIRフィルタの
周波数特性の逆フーリエ変換から、そのFIRフィルタのインパルス応答を求めます。
e-jωTの振幅特性は全周波数領域にわたり1となり、位相特性はωに比例して直線位相なので、e-jωTを使用して
ローパスフィルタの係数を求めます。
1・e-jωLT(-ωc ≦ ω ≦ ωc)
0 (-ωc > ω , ω > ωc)
0 (-ωc > ω , ω > ωc)
インパルス応答の係数を求めるために、e-jωLTと共役のejωnTを使用して逆フーリエ変換を行うと、
ωs = 2π/T (T : サンプル周期 L : 遅延数 n:0~L)
|
カットオフ周波数をωcとし、 ωc < ωs /2
周波数振幅特性は、±ωcの範囲 = 1
それ以外 = 0
|
|
よって、積分する領域は、±ωcの範囲となります。
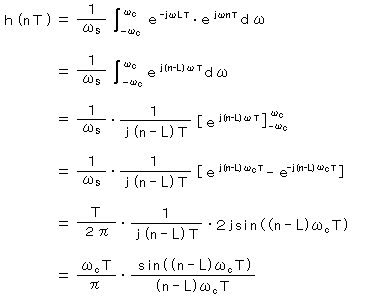
Top項目へのアクセス