- ホーム
- >実 験
- >境界検索(最小二乗近似)
|
実験 >画像処理基本ソフト >画像処理・処理速度の比較 |
輪郭を追跡
計測データの最小二乗近似方程式 |
|
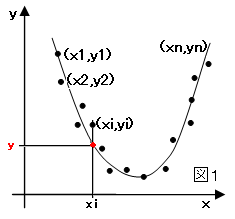
測定したデータにバラツキがある場合、データのバラツキを補間して 入力と出力の関係を求める場合に使用されます。 図1のようにN個の計測データ(x1,y1)(x2,y2)・・・ (xi,yi)・・・(xn,yn)があり、データのバラツキを補間した二次曲線が、 y=ax2+bx+cで表現されるとします。 この二次曲線の係数a、b、cを求める方法として最小二乗近似があります。 補間した二次曲線方程式上のxに値を与えると二次曲線上の補間されたyの値を求めることができます。 補間する方程式として、下記があります。過去に6次方程式までを使用しました。 y=ax+b y=ax2+bx+c y=ax3+bx2+cx+d y=ax4+bx3+cx2+dx+f |
|
| 左画像はモノクロの画像から画像を明と暗に二値化し、二値画の輪郭を追跡しました。 傾斜部分がある範囲内にあるかを検査できます。 | 右画像は粒子解析を行い粒子の点列座標を基に最小二乗近似を用いて形状の一部の輪郭の方程式を求め座標を計算しました。 | |
生画像 |
 |
 |
二値画像 |
映像の積算を行い平均化後二値化処理

|
輝度の微分処理を行いb>二値化処理

|
|---|
輪郭抽出 |
二値画の輪郭を追跡しその座標を取得
|
粒子の点列座標を基に最小二乗近似を用いて輪郭描画(緑色)

|
|---|
|
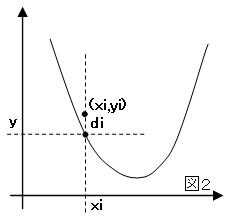
入力データxiのとき出力がyi、二次曲線との距離をdiとします。
このときdiの二乗の和(誤差)が最小となるように求めます。
D=∑ni=1(di2) =∑ni=1(yi-(axi2+bxi+c))2
|
|
yiの値が極大、極小となるのは、偏微分=0なので
a、b、cに関して偏微分=0を求めます。∂D/∂a=(∂D/∂Z)(∂Z/∂a)
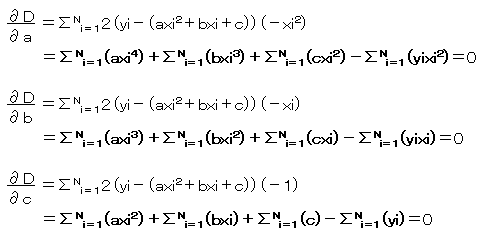
上記の連立方程式をといて、係数a、b、cを求めます。
行列を使用して連立方程式から正規方程式を求めると
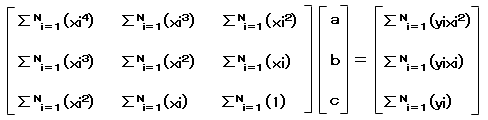
ある行列をAで表すと逆行列はA-1で表され、AA-1=1なので
正規方程式に逆行列をかけると、係数a、b、cは下記で求まります。
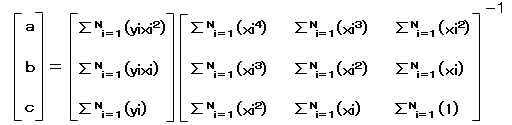
逆行列を求めるには、

Aの行列式と余因子行列を用いて
(余因子Aijは行列Aから第i行、第j列を取り除いた 正方行列の行列式に(-1)i+jをかけたものです。)
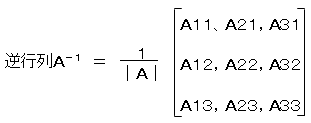
行列式|A|を余因子を用いて展開すると
a、b、cに関して偏微分=0を求めます。∂D/∂a=(∂D/∂Z)(∂Z/∂a)
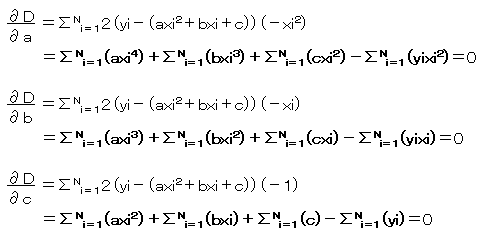
上記の連立方程式をといて、係数a、b、cを求めます。
行列を使用して連立方程式から正規方程式を求めると
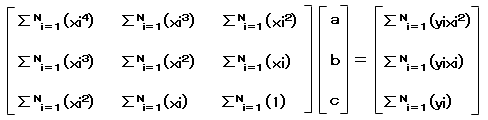
ある行列をAで表すと逆行列はA-1で表され、AA-1=1なので
正規方程式に逆行列をかけると、係数a、b、cは下記で求まります。
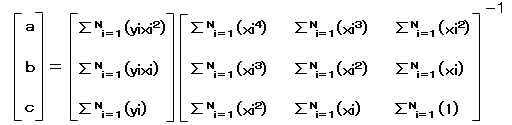
逆行列を求めるには、

Aの行列式と余因子行列を用いて
(余因子Aijは行列Aから第i行、第j列を取り除いた 正方行列の行列式に(-1)i+jをかけたものです。)
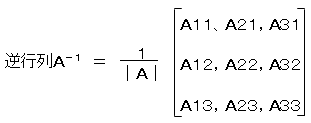
行列式|A|を余因子を用いて展開すると
行列式|A|=a11A11+a12A12+a13A13
|
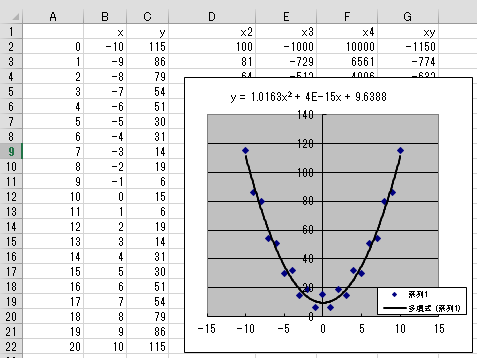
仮のデータに対し、Excelで最小二乗近似を使用して係数を求めました。
y=x2+10に±5の誤差を加えました。
a = 1.0163
b = 4E-15 c = 9.6388 |
|
|
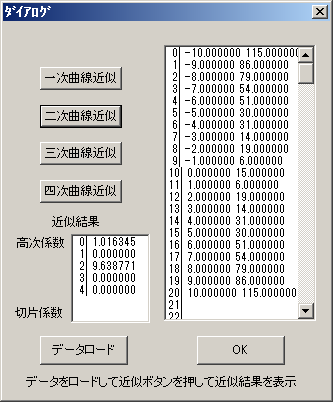
最小二乗近似プログラムを作成、同じデータを使用して係数を求めました。
ほぼ、同じ値となりました。
a = 1.016345
b = 0 c = 9.638771 |
|
Top項目へのアクセス