- ホーム
- >実 験
- >FFT変換>FFT変換例
|
実験 >FFT変換 |
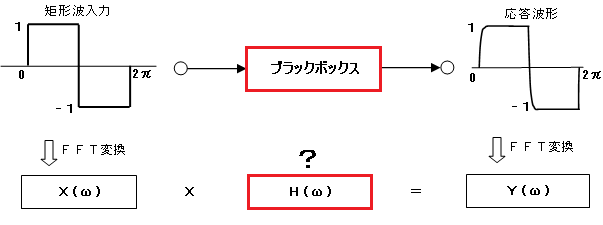
FFT変換プログラムを作成しました。矩形波のFFT変換、逆FFT変換を実行します。
その応用として、システムの同定を行います。入力波形と出力波形のFFT変換結果から、
ブラックボックスの伝達特性を求めます。
その応用として、システムの同定を行います。入力波形と出力波形のFFT変換結果から、
ブラックボックスの伝達特性を求めます。
FFT変換プログラムを作成、FFT変換例を次ページに表示します。
FFT変換プログラムに入力する波形は、0~2π、±1の矩形波です。
|
|
|
下記に±1の矩形波をFFT変換し、その結果をFFT変換プログラムのダイアログ、出力データリストに
表示しました。
表示しました。
|
FFT検証用実行条件 FFTのサンプルデータ数 サンプリング周波数 データ周波数
(周期=1024mS)
区間0~511の値 区間512~1023の値 窓関数 |
=1024 =1KHz =0.976Hz =1.0 =-1.0 =無し |
|
(波形作成プログラムにて矩形波(1Hz、±1)を*.CSVファイルへ出力し、そのファイルを読み込んでFFT変換を実行、
ダイアログの下方のリストに出力データを表示しました。FFT変換を行うとサンプリング周期*サンプリング点数を
周期とする基本波と整数倍の高調波の振幅スペクトル、位相スペクトルを求めることができます。)
下記は、入力波形(±1の矩形波)と、FFT変換後の周波数スペクトルのグラフです。
基本周波数振幅4/π =1.273、20log(1.273)=2dB
第3高調波振幅4/3π =0.424、20log(0.424)=-7.5dB
第5高調波振幅4/5π =0.255、20log(0.255)=-11.9dB
第7高調波振幅4/7π =0.182、20log(0.182)=-14.8dB
第3高調波振幅4/3π =0.424、20log(0.424)=-7.5dB
第5高調波振幅4/5π =0.255、20log(0.255)=-11.9dB
第7高調波振幅4/7π =0.182、20log(0.182)=-14.8dB
下記は、入力波形(±1の矩形波)と、FFT変換後の周波数スペクトルのグラフです。
|
|
先ず、FFT変換により求めた周波数スペクトルを合成して、7次迄ですが何となく元の矩形波に合成されることを確認します。
FFTの演算結果の基本波(振幅,位相)、第三高調波の(振幅,位相)~第7高調波の(振幅,位相)を使用して、
EXCELで下式の演算を行いました。xは0~360°をラジアンへ変換した値
下記に、EXCELで計算した表とグラフを表示します(L:振幅、P:位相)。
EXCELで下式の演算を行いました。xは0~360°をラジアンへ変換した値
基本波振幅 = 1.273*COS(1x+θ1) :θ1=-1.568
第3高調波振幅 = 0.424*COS(3x+θ3) :θ3=-1.562
第5高調波振幅 = 0.255*COS(5x+θ5) :θ5=-1.555
第7高調波振幅 = 0.182*COS(7x+θ7) :θ7=-1.549
合成波形 = 基本波振幅 +第3高調波振幅 +第5高調波振幅 +第7高調波振幅
第3高調波振幅 = 0.424*COS(3x+θ3) :θ3=-1.562
第5高調波振幅 = 0.255*COS(5x+θ5) :θ5=-1.555
第7高調波振幅 = 0.182*COS(7x+θ7) :θ7=-1.549
合成波形 = 基本波振幅 +第3高調波振幅 +第5高調波振幅 +第7高調波振幅
下記に、EXCELで計算した表とグラフを表示します(L:振幅、P:位相)。
|
|
|
|
FFT変換により求めた各次数の実数と虚数を入力して、FFT逆変換を行います。
|
各次数の振幅と位相をFFT逆変換 |
|
FFT逆変換した出力データの波形です。
|
|
Top項目へのアクセス